Pensándolo bien...

El cuerpo humano permanece inalterado solamente bajo dos operaciones de simetría: la identidad y la reflexión en un plano vertical, que es la que se denomina simetría bilateral. La primera de ellas, I, deja a cualquier cuerpo inalterado cuando se le aplica y la segunda, r supone una reflexión que reproduce la otra mitad en que queda dividido, en este caso el cuerpo, cuando imaginariamente situamos un espejo que pasa de arriba abajo desde la cabeza hasta los pies. El interrogante de interés es ¿qué ocurre cuando se aplican estas transformaciones, identidad y reflexión, sucesivamente? Reflexión y después identidad, y viceversa, es lo mismo que reflexión sólo. Si se aplican dos reflexiones sucesivas obtenemos, también,  lo mismo, es decir, es equivalente a la transformación que llamamos identidad. Podemos disponer una tabla, como la de multiplicar números, que exhaustivamente contenga todas las posibles duplas de transformaciones de simetría. Así

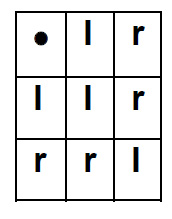
Hemos indicado con el signo · la operación sucesiva de dos transformaciones, una tras otra (la más próxima es la primera que se aplica y la más lejana se aplica al resultado que resulta de aplicar la primera). En nuestro caso, por ejemplo

 

r · r (cuerpo humano) = I (cuerpo humano) = cuerpo humano

Podemos, fácilmente, comprobar que esta tabla de multiplicación forma un grupo, porque no hay mas que comprobar que satisface las propiedades de un grupo:

1.- Clausura (cerradura), ya que la combinación sucesiva de dos transformaciones de simetría, es una transformación de simetría.

2.- Asociatividad: Para tres operaciones de simetría, p.ej, I r y r podemos agruparlas de  cualquiera de las formas que implican los paréntesis siguientes. I·r·r = I·(r·r) = (I·r) ·r, y el resultado que obtenemos es el mismo.

3.- Hay un elemento identidad: porque la identidad es una operación de simetría.

4.- Existe el inverso: en nuestro caso, cada una de las operaciones de simetría actúa como su inversa, dado que: r·r = I¸ I·I = I

 

Así pues, el grupo de simetrías del cuerpo humano, solamente contiene dos elementos, la identidad y la reflexión en un plano. Todas las transformaciones de simetría de cualquier sistema forman un grupo, siempre.

Lo curioso del caso es que a diferencia de la mayoría de los descubrimientos matemáticos, que planificada y denodadamente se buscan, nadie buscó, nunca, la teoría de grupos, ni siquiera una teoría de la simetría. El concepto surgió, como de forma espontánea, que no azarosa. No apareció buscando alguna solución a ninguna ecuación algebraica. El concepto cristalizó en el contexto de la teoría del caos. Su historia es tumultuosa. Le precedieron casi cuatro mil años de curiosidad. Tiene aplicaciones en campos científicos muy diversos como la astrofísica, en el estudio de los quarks o la criptografía. Históricamente está relacionada con la teoría de las ecuaciones algebráicas, la de números y la geometría. Matemáticos como Euler, Gauss, Lagrange, Abel y Galois implican sus nombres en su desarrollo. Se atribuye a Galois la denominación como grupo. Otros muchos matemáticos lo trataron después. Hoy nos beneficiamos de ello. Los cálculos cuánticos se benefician, ¡de qué manera!, de las simplificaciones que implica la simetría. De no ser por ella, buena parte de los problemas serían inabordables. Sin ir más lejos, es determinante la simetría para conjeturar las propiedades físicas: si un sistema molecular tiene una propiedad vectorial, debe estar situada sobre todos los elementos de simetría que tenga, dado que es la única forma en que la magnitud física, a la que no se puede ver afectada, permanezca inalterada ante cualquier operación  de simetría. De tener dos elementos de simetría no coincidentes, imaginemos un plano y un eje perpendicular a ese plano, el momento dipolar tendría que estar sobre ambos para no verse modificado. La única solución es que no lo tenga, ante la imposibilidad de satisfacer la condición. Y esto tiene consecuencias. Simplemente analizando los elementos de simetría, se deducen propiedades posibles o se niega su existencia. Si una molécula o tuviera momento dipolar, ni se generara una asimetría de la carga como consecuencia de algún movimiento, no podría exhibir espectro infrarrojo. Y esto se deduce sin llevar a cabo ningún experimento. ¡Realmente, extraordinario!