Pensándolo bien...

La idea de que Bernhard Riemann, el influyente matemático alemán del siglo XIX, buscaba una fórmula o función capaz de probar la existencia de Dios es una afirmación que se mueve entre la especulación filosófica, el simbolismo y el mito intelectual. No hay pruebas documentales directas de que Riemann se propusiera literalmente encontrar una “fórmula de Dios”, como a veces se sugiere en círculos esotéricos o de divulgación. Sin embargo, una exploración cuidadosa de su vida, sus ideas matemáticas y su contexto cultural puede arrojar luz sobre por qué esa interpretación ha capturado la imaginación de muchos.

El siglo XIX fue una época de profundas transformaciones en la Ciencia, la filosofía y la teología. El racionalismo heredado del Iluminismo convivía con una renovada búsqueda espiritual. En medio de esta tensión, Bernhard Riemann (1826–1866) destacó como un matemático que no sólo revolucionó la geometría y el análisis, sino que mostró una sensibilidad religiosa y filosófica inusual entre sus colegas. Si Riemann buscaba una función capaz de probar la existencia de Dios, nos obliga a navegar entre la historia, la metafísica y los límites del pensamiento humano.

Riemann nació en una familia profundamente piadosa. Su padre era un pastor luterano que inculcó a sus hijos una formación espiritual rigurosa. Desde niño, Riemann mostró una devoción sincera y una inclinación al recogimiento. Aunque su genio matemático fue precoz, nunca abandonó su sensibilidad religiosa. Se ha señalado que Riemann llevaba consigo una Biblia incluso durante sus estudios universitarios, y que a menudo leía textos teológicos además de tratados matemáticos.

Su vida fue corta y discreta, marcada por la introspección. Murió a los 39 años, de tuberculosis. En sus cartas y escritos, la figura de Dios aparece no como un objeto de demostración, sino como una presencia que le acompañaba en su contemplación del infinito. Esta disposición religiosa no impide que su obra contenga profundas implicaciones metafísicas que, según algunos, podrían leerse como un intento de encontrar orden, y quizás divinidad, en el cosmos matemático.

En la tradición filosófica occidental, desde Pitágoras hasta Newton, muchos pensadores han entendido la Matemática como un lenguaje divino o como una vía hacia la comprensión del orden superior del universo. Leibniz, por ejemplo, afirmó que “cuando Dios calcula y piensa las cosas, el mundo se hace”. En este sentido, no sería extraño que Riemann, formado en esa herencia intelectual, entendiera que las estructuras matemáticas que descubrimos en la naturaleza no son arbitrarias, sino reflejos de un diseño superior.

Riemann no escribió tratados teológicos, pero en su célebre Habilitationsvortrag de 1854, que es el discurso de habilitación que cambió para siempre la geometría, encontramos una pista. En ese texto, titulado “Sobre las hipótesis que yacen en los fundamentos de la geometría”, Riemann no sólo amplía la noción de espacio, sino que concluye con una reflexión sobre la finitud del conocimiento humano. Afirma que el espacio físico podría tener una estructura no euclidiana, pero que su forma definitiva depende de “los datos empíricos”, los cuales “sólo pueden ser determinados por la experiencia”. Y, sin embargo, hay algo más que su forma de expresarse, porque sugiere que detrás del mundo mensurable hay un misterio que sólo puede ser intuido, no demostrado.

La fama de Riemann entre los matemáticos contemporáneos se debe, en gran parte, a su célebre Hipótesis de Riemann, propuesta en 1859. En su artículo “Sobre el número de primos menores que una cantidad dada”, Riemann introduce lo que hoy llamamos la función zeta de Riemann, una función compleja cuyas propiedades están misteriosamente relacionadas con la distribución de los números primos.

La función zeta, definida inicialmente como:

para ℜ(s)>1, puede extenderse mediante prolongación analítica al plano complejo. Riemann conjetura que todos los ceros no triviales de esta función tienen parte real igual a 1/2, es decir, están alineados simétricamente sobre la línea crítica. Esta alineación perfecta no ha podido ser demostrada aún, y constituye uno de los problemas más fundamentales y enigmáticos de la matemática moderna.

La función zeta de Riemann es uno de los objetos más profundos y misteriosos de las Matemáticas. Su interpretación depende del nivel desde el cual la abordemos: aritmético, analítico, geométrico, físico o incluso filosófico. Para números reales s>1, la función zeta se define como una serie infinita:

Esto significa que para cada número s, se suman los inversos de todas las potencias n^s, con n desde 1 hasta infinito. Por ejemplo:

Este valor, sorprendentemente, tiene una expresión compacta: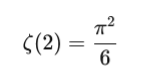  

Este tipo de relaciones entre la función zeta y π fue una de las primeras sorpresas que atrajo el interés de los matemáticos.

Una de las propiedades más profundas de la función zeta es su relación con los números primos. A través del producto de Euler, se puede expresar como: 

Este producto infinito muestra que los primos están "codificados" en la función zeta. La función zeta actúa como un “sensor” que detecta la estructura oculta de los números primos. Es como una caja negra que, cuando se analiza, revela información sobre cómo se distribuyen los primos.

Riemann extendió la función zeta al plano complejo, mediante prolongación analítica. Así, en vez de solo números reales s, se considera que s es un número complejo: s = σ + t i, donde σ es la parte real y t la imaginaria. En este contexto, la función zeta tiene:

• Ceros triviales en los enteros negativos pares: −2,−4,−6,…
• Tiene ceros no triviales en una franja crítica: 0 < ℜ(s) < 1

La famosa Hipótesis de Riemann postula que todos los ceros no triviales están sobre la línea ℜ(s)=1/2. En el plano complejo, la función zeta vibra como una cuerda cósmica. Sus ceros indican puntos de cancelación en su estructura armónica. La simetría de estos ceros parece señalar una ley universal aún no demostrada.

Algunos físicos han descubierto que los ceros de la función zeta tienen similitudes con los niveles de energía de sistemas cuánticos caóticos. En particular, las estadísticas de los ceros no triviales de ζ(s) son similares a las del espectro de energías de ciertos sistemas cuánticos, de aquí la conexión con las matrices aleatorias. Esto sugiere que la función zeta puede describir, de forma abstracta, sistemas físicos reales. Algunos especulan que puede haber una interpretación cuántica de los ceros de Riemann.

En Geometría, se han desarrollado versiones de la función zeta para curvas, superficies y espacios definidos sobre cuerpos finitos. Estos “análogos geométricos” ayudan a entender ζ(s) como el resultado de contar estructuras en geometrías abstractas. La función zeta de Riemann puede verse como una “sombra” de una geometría aún no completamente entendida. Algunos buscan una variedad geométrica oculta cuyo espectro o forma dé origen a la función zeta.

Aunque no es parte de la matemática formal, muchos han visto en la función zeta una estructura casi mística. Tiene características que fascinan, como que relaciona sumas infinitas con productos infinitos, une lo continuo y lo discreto y deambula por el análisis, álgebra, geometría y física. Para algunos, la función zeta es un arquetipo del orden oculto del universo. Su belleza, simetría y misterio han llevado a compararla con una especie de “firma de Dios” inscrita en el lenguaje de los números.

Las Aplicaciones abarcan desde la criptografía y teoría de números, donde la zeta es central para entender la distribución de los números primos, que son la base de sistemas criptográficos modernos. En estadística y física estadística, donde aparece en cálculos de entropía, energía, y sistemas en equilibrio térmico. En Matemática ya que la teoría analítica de números gira en torno a su comportamiento.

La función zeta de Riemann es mucho más que una simple suma. Es una entidad matemática profundamente rica, con tentáculos que se extienden por toda la Ciencia y la filosofía. Puede verse como una suma infinita con comportamiento ordenado, como un registro secreto de los números primos, como un objeto complejo con simetrías sorprendentes, como una vibración armónica que parece tener eco en la física cuántica o como una estructura metafísica que conecta orden y caos, finitud e infinito. Entenderla del todo, quizá, implique no solo Matemáticas, sino una ampliación de nuestro concepto de conocimiento. Como decía David Hilbert "Si yo despertara después de dormir mil años y me dijeran que la Hipótesis de Riemann fue resuelta, preguntaría primero: ¿Cuál fue la respuesta?"

La pregunta que surge a los humanos restantes es: ¿por qué esta función, vinculada con los números primos, auténticos átomos de la aritmética, exhibe una simetría tan precisa, tan elegante, tan... divina? Muchos matemáticos han confesado que la función zeta parece “revelar” una armonía profunda en los fundamentos del número. Alain Connes, uno de los padres de la geometría no conmutativa, ha sugerido que resolver la hipótesis de Riemann sería como tocar “la música del universo”.

Desde el Renacimiento, la noción de “teología natural” buscó demostrar la existencia de Dios mediante la razón y la observación de la Naturaleza. En este marco, las matemáticas han sido vistas como pruebas de la inteligencia divina que subyace en el Cosmos. Kepler creyó ver en las órbitas planetarias la geometría sagrada. Descartes sostuvo que las verdades matemáticas proceden directamente del entendimiento divino. ¿Podemos incluir a Riemann en esta tradición? Algunos indicios permiten suponer que sí. Aunque nunca afirmó explícitamente que su obra fuera una búsqueda de Dios, hay una confluencia entre su religiosidad personal y la profundidad casi mística de sus intuiciones matemáticas. Su obra parece guiada por una confianza absoluta en que el Universo es legible, que posee un orden, y que ese orden puede descubrirse, aunque nunca del todo, wmediante símbolos, funciones y estructuras. En este sentido, la función zeta de Riemann puede interpretarse como un espejo de lo divino: una fórmula que toca los bordes de lo absoluto, una “huella” de Dios en el lenguaje del infinito.

En tiempos recientes, ha crecido la fascinación con la idea de que Riemann, consciente o inconscientemente, estuvo cerca de hallar la “fórmula de Dios”. Esta expresión, popularizada por películas, novelas y documentales, ha sido usada para referirse a ecuaciones que contengan la totalidad del orden cósmico, una especie de “teoría del todo” al estilo de Einstein o Stephen Hawking.

En este contexto, la función zeta se ha convertido en candidata mística a esa función suprema. ¿Por qué? Porque parece reunir lo caótico, la distribución aparentemente aleatoria de los números primos, con lo ordenado, la simetría profunda de sus ceros, es decir, une el azar con la necesidad. En términos filosóficos, une el devenir con el ser. ¿No es eso precisamente lo que haría una fórmula divina? A pesar de lo seductor de esta interpretación, conviene matizar, porque no hay evidencia de que Riemann creyera que su función probara la existencia de Dios. Pero tampoco es casual que tantos matemáticos y filósofos hayan visto en ella una belleza “trascendente”, algo que excede la razón y toca lo sagrado.

La pregunta sobre si Riemann quería encontrar una función capaz de probar la existencia de Dios tal vez deba reformularse. No se trata de que él concibiera una fórmula con la intención explícita de resolver la cuestión teológica, como un silogismo con resultado divino. Más bien, Riemann parecía intuir que las Matemáticas, en su profundidad más abstracta, nos acercan a una realidad más alta, invisible y unificadora.

Su obra se enmarca dentro de una tradición que ha visto en la matemática no sólo una ciencia exacta, sino una forma de contemplación. En ese sentido, la función zeta, como la música de Bach o la geometría de una flor, puede interpretarse como una revelación parcial del misterio del ser. Riemann, hombre de fe y Ciencia, tal vez no buscaba probar a Dios, sino encontrar su reflejo en la estructura misma del Cosmos. Y en esa búsqueda, dejó una de las funciones más enigmáticas y bellas de la historia de la humanidad.

Sopa de letras: RIEMANN Y LA FUNCIÓN DE DIOS

Soluciones: BATERÍAS CUÁNTICAS