Con matices importantes  pueden existir análogos moleculares de los puntos de Lagrange, pero no como “puntos geométricos fijos en el espacio”, sino como configuraciones de equilibrio en paisajes de energía potencial. Es un análogo funcional y conceptual, no literal.

Un punto de Lagrange clásico es un punto de equilibrio dinámico, definido en un campo efectivo (fuerzas + marco no inercial), que puede ser estable o inestable. En el mundo molecular no hay marcos rotantes macroscópicos, pero sí superficies de energía potencial (PES), donde los núcleos se mueven como “partículas” bajo fuerzas derivadas del potencial electrónico. El análogo no es espacial, sino energético y configuracional.

En química cuántica, una molécula se describe mediante una superficie de energía potencial en función de las posiciones nucleares. En esa superficie existen mínimos → extructuras estables, puntos de silla → estados de transición, valles y crestas → caminos de reacción. Estos puntos cumplen un papel muy parecido a los puntos de Lagrange.

Ejemplo claro lo tenemos en el ion H₃⁺. El ion H₃⁺ es paradigmático, porque tiene tres protones, un solo estado electrónico compartido. La estructura equilátera del ion corresponde a un mínimo colectivo donde ninguna pareja por sí sola sería estable y la estabilidad surge del equilibrio global. Esto es muy cercano a un L4/L5 molecular ya que es una estabilidad que no existe por pares, sino por la configuración conjunta.

Los estados de transición son equivalentes a puntos de Lagrange inestables. En una reacción química, el estado de transición es un punto de equilibrio inestable y una pequeña perturbación lleva a reactivos o productos. Esto es formalmente idéntico a L1, L2 o L3 en el problema de tres cuerpos. No se “ocupa” permanentemente, pero organiza la dinámica.

Los análogos aún más directos los tenemos en las moléculas no covalentes, como complejos de van der Waals, enlaces de hidrógeno y química supramolecular, donde aparecen regiones del espacio donde una partícula (átomo, ion, molécula) queda confinada por fuerzas opuestas. No hay enlace clásico, pero sí equilibrio geométrico inducido. Son auténticos “puntos de Lagrange blandos”.

A diferencia del caso gravitatorio, los núcleos no están fijos, existen fluctuaciones cuánticas y el equilibrio es siempre probabilístico, no puntual. Por eso el análogo molecular nunca es un punto exacto, sino una región de alta densidad de probabilidad.

En suma sí que existen análogos moleculares funcionales de los puntos de Lagrange, no como puntos geométricos fijos en el espacio, pero sí como mínimos colectivos, puntos de silla, regiones de confinamiento dinámico y organizadores de la dinámica molecular.

La idea profunda compartida es que un sistema puede ser estable no porque sus partes se atraigan directamente, sino porque la configuración global del campo lo permite.

Ejemplo: una superficie de energía potencial con dos mínimos y un punto de silla

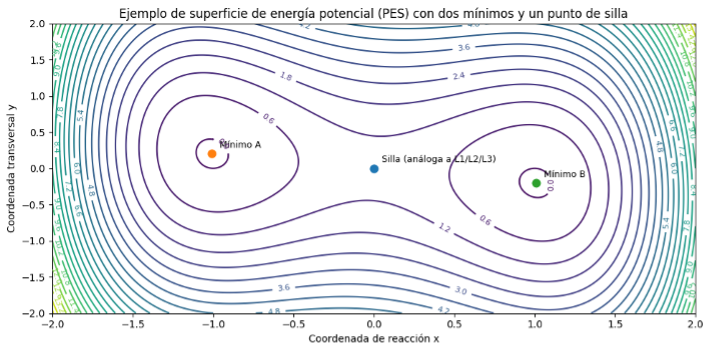
Definimos la energía potencial como:

V (x,y) = (x² −1)² + y² + kxy

Donde  x es la coordenada de reacción (progreso de A → B),  y es la coordenada transversal (deformación o vibración), k es un parámetro de acoplamiento (por ejemplo, k = 0,4).

Puntos críticos (análogos a puntos especiales)

Los puntos críticos se obtienen resolviendo la condición:

∇V = 0

es decir,

                                ,         .

De la segunda ecuación se obtiene:

Sustituyendo en la primera ecuación:

.

De aquí se sigue que:

                                                         x = 0        o               .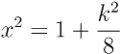

Por tanto, existen tres puntos críticos:

Punto de silla (análogo a L1/L2/L3):

(x,y) = (0,0).

Dos mínimos (pozos A y B):

Para k = 0,4 se obtiene aproximadamente:

                       Mínimo A ≈ (−1,01, +0,20),          Mínimo B ≈ (+1,01, −0,20).

Estabilidad

La estabilidad se analiza mediante el Hessiano, es decir, la matriz de segundas derivadas del potencial.

 En el punto (0,0) aparece una curvatura positiva y otra negativa, lo que caracteriza un punto de silla, es decir, un equilibrio inestable.

 En los mínimos, ambas curvaturas son positivas, lo que indica un equilibrio estable.

Lectura tipo Lagrange

Los mínimos juegan el papel de regiones estables, de forma análoga a los puntos L₄ y L₅ del problema gravitatorio de tres cuerpos.

El punto de silla organiza la dinámica del sistema: actúa como un cuello de botella por el que se produce el paso de A a B, de manera funcionalmente análoga a los puntos

L₁, L₂ o L₃.

En química, este punto de silla se interpreta como el estado de transición de la reacción.

Sopa de letras: PUNTOS DE LAGRANGE MOLECULARES

Soluciones: RUPTURA DE BORN OPPENHEIMER