Pensándolo bien...

Transformaciones repentinas y radicales de sustancias conocidas por la humanidad durante eones, como la congelación de agua y la sopa que se preparaba sobre un fuego, permanecieron misteriosas hasta bien entrado el siglo XX. Los científicos observaron que las sustancias suelen cambiar gradualmente: Calienta un poco la colección de átomos y el material se expande un poco. Pero cuando se lleva un material más allá de un punto crítico, se convierte en otra cosa distinta por completo. Las transiciones de fase son fenómenos físicos en los que un sistema cambia de un estado o fase a otro, respondiendo a cambios en variables externas como la temperatura, presión o campo magnético.

El modelo de Ising es un modelo matemático en física estadística y teoría del magnetismo que se utiliza para describir la transición de fase en sistemas magnéticos. Fue introducido por el físico alemán Wilhelm Lenz en 1920 y su alumno Ernst Ising lo estudió en su tesis doctoral en 1924. Se asume que el sistema está compuesto por una red regular de sitios (o nodos) que pueden ser en una, dos o tres dimensiones. La configuración más estudiada es la red bidimensional cuadrada. Cada sitio de la red contiene una variable de espín s_i, que puede tomar dos valores: +1 o −1. Estos valores representan el momento magnético de un átomo que puede apuntar hacia arriba (positivo) o hacia abajo (negativo). La energía del sistema en el modelo de Ising está dada por la siguiente función Hamiltoniana 

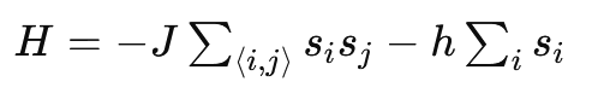
donde:

• J es la constante de interacción que determina la fuerza y el signo de la interacción entre espinesvecinos.
• < i, j > denota la suma sobre pares de sitios vecinos.
• h es el campo magnético externo aplicado al sistema.
• s_i​ y s_j​ son los espines en los sitios i y j.

El comportamiento del Modelo conlleva que la interacción ferromagnética se describe como si J>0, de forma que los espines vecinos tienden a alinearse en la misma dirección, favoreciendo la magnetización neta.  Si J<0, los espines vecinos tienden a alinearse en direcciones opuestas, evitando una magnetización neta.

El modelo de Ising muestra una transición de fase de segundo, también conocida como transición continua, que es un tipo de transición en la que el cambio entre dos fases de un sistema ocurre de manera continua y sin liberación de calor latente. Estas transiciones se caracterizan por la continuidad de la primera derivada de la energía libre respecto a una variable termodinámica, como la temperatura, mientras que la segunda derivada es discontinua. A diferencia de las transiciones de primer orden (como la fusión o la ebullición), no hay un cambio abrupto en la estructura del material, sino que las propiedades del sistema cambian gradualmente) en dos dimensiones en ausencia de campo magnético externo (h=0). A una temperatura crítica T_c ​, el sistema pasa de una fase ordenada (donde los espines están alineados) a una fase desordenada (donde los espines están orientados aleatoriamente).

La solución del modelo en una dimensión no muestra transición de fase a temperatura finita. En 1944, Onsager encontró una solución exacta para el modelo bidimensional sin campo magnético externo, demostrando la existencia de una transición de fase. El modelo de Ising se ha extendido para estudiar fenómenos en otras áreas como redes neuronales, economía, biología y sistemas complejos. 

Dado que las soluciones exactas solo son posibles en casos muy específicos, se utilizan técnicas de simulación numérica, como el método de Monte Carlo, para estudiar el comportamiento del modelo de Ising en redes de mayor dimensión y bajo diversas condiciones. El modelo de Ising es fundamental en la física teórica y ha proporcionado una comprensión profunda de las transiciones de fase y el comportamiento crítico en sistemas magnéticos y otros sistemas complejos.

Imagen creada con Chat GPT con DALL-E

La clave matemática para romper transiciones de la fase se formuló hace unos 100 años y ha transformado las ciencias naturales. El modelo Ising, fue propuesto inicialmente como una imagen de dibujos animados de imanes.  Imaginen una cuadricula con múltiples casillas conteniendo unas flechas hacia arriba o hacia abajo. Podemos colorearlas de azul y rojo, respectivamente a las orientadas hacia arriba y hacia abajo. El juego consiste en cambiar de un tipo a otro, al azar, lo que se puede programar fácilmente haciendo uso de un generador de números pseudoaleatorios. El espectáculo es curioso. Imaginariamente representa algún proceso que provoca el cambio, sin atender a ninguna variable exgerna ni de forma regular, solo aleatoriamente. Con esos valores para los espines (+1 y -1) se puede evaluar con la fórmula incluida más atrás, la interacción. Ahora se utiliza usualmente como un modelo simple de sistemas físicos para estudiar desde qué ocurre con la mosca de la fruta, al comportamiento del organismo como modelo de biología. Las aplicaciones han sido muy numerosas e interesantes. Hasta se ha aplicado como modelo de terremotos, proteínas, cerebros e incluso segregación racial.

En 1920 el físico alemán Lenz, estudió la pérdida de poder atractivo de un imán al calentarlo por encima de cierta temperatura. Imaginó un imán como compuesto de una trama de flechas apuntando hacia arriba o hacia abajo, que representaban a los átomos, tratados como imanes con polos norte y sur y, por ende, orientaciones. Ahora bien, como las flechas influyen en los vecinos, tratando de forzarlas a que tomen la misma orientación, ocurre que si la mayoría de átomos se alineaban, sus campos magnéticos se fusionaban y el material se comportaría como un imán. En cambio, si las flechas se mezclaban uniformemente unas y otras se neutralizarían y no exhibirían magnetismo. En esa trama donde se situaban las flechas tenía lugar, pues, una lucha entre el calor y el magnetismo. El primero constituyendo el azar de las partículas, que pretendía provocar el desorden y el magnetismo que se resistía al caos. Lenz supuso que a baja temperatura dominaba el orden magnético, mientras que con el concurso del calor el empuje aleatorio afectaría a la cooperación atómica y tendría explicación la observación de Pierre Curie de que los imanes calientes pierden el efecto magnético.

Precisamente, Lenz encargó a su estudiante, Ising, que trabajara el tema. Ising simplificó el escenario omitiendo la tridimensionalidad y limitándose a una cadena lineal y plasmó con flechas el esquema en el que cada átomo incidía en sus dos vecinos inmediatos. Propuso el modelo 1D de Ising y la cadena que representaba no deja de estar magnetizada. A todas las temperaturas se mantiene el efecto. Los resultados se mantuvieron para las hojas 2D  y los bloques 3D en el trabajo publicado en 1925, de forma que el modelo no representaba adecuadamente el comportamiento de los imanes reales, como había propuesto Curie. Pese al fracaso, el modelo se mantuvo en vigor y en 1940 Onsager, físico teórico y posteriormente Premio Nobel calculó la proporción de átomos que probablemente apuntaban sus espines en una dirección a cualquier temperatura y en el caso 2D, en la que se consideran cuatro vecinos. La conclusión fue que en 2D las flechas alineadas y el magnetismo es compatible a bajas temperaturas, mientras que el desorden se da cuando se supera una temperatura crítica. Se vio como una caricatura de la realidad, pero resulta que las mediciones de argón y helio, reveló que Onsager tenía razón. Los denominados exponentes críticos, que describen el comportamiento de las propiedades físicas cerca de la transición de fase, son universales, lo que significa que son los mismos para todas las sustancias que pertenecen a la misma clase de universalidad y describen la velocidad a la que cambian varias propiedades en el periodo de ejecución de las transiciones de fase. Estos exponentes describen los detalles de como tienen lugar los procesos de cambios de fase y como los colectivos (islas) van creciendo al enfriarse o calentarse el sistema acercándose a la transición de fase.

A la temperatura crítica, conviven islas de todos los tamaños, desde puntos a continentes. Aquí, una flecha puede inducir la vuelta de otra flecha distante, pese a no ser vecinos lo que indica la superación de los detalles microscópicos.  A este nivel impera el número de dimensiones y las simetrías, al margen de que a nivel microscópico sigan siendo átomos o moléculas.

El modelo de Ising ha jugado un papel fundamental en la Ciencia, especialmente en el campo de la mecánica estadística y la teoría de la materia condensada. Representa uno de los modelos teóricos más importantes para entender las transiciones de fase y los fenómenos críticos. Ha aportado contribuciones muy significativas a la comprensión de las transiciones de fase proporcionando una descripción simple y clara de las transiciones de fase de segunda orden (transiciones continuas). Ayuda a entender cómo los sistemas cambian de un estado ordenado a un estado desordenado al variar la temperatura. Ha contribuido al desarrollo de la teoría de la renormalización, una herramienta matemática fundamental para estudiar los comportamientos críticos y las transiciones de fase. Esta teoría permite comprender cómo las propiedades macroscópicas de un sistema emergen de sus interacciones microscópicas. Ha aportado descripción de propiedades críticas y exponentes universales, que describen cómo las propiedades físicas divergen cerca del punto crítico. Estos exponentes son universales, es decir, se aplican a una amplia variedad de sistemas físicos, no solo al modelo de Ising. Ha impulsado simulaciones y métodos computacionales, que han servido como banco de pruebas para desarrollar y perfeccionar métodos de simulación numérica, como el algoritmo de Monte Carlo. Estas técnicas computacionales son esenciales para estudiar sistemas complejos donde los métodos analíticos no son aplicables. Ha tenido múltiples aplicaciones interdisciplinarias, ya que aunque originalmente formulado para describir el magnetismo, el modelo de Ising ha encontrado aplicaciones en diversas áreas fuera de la Física, incluyendo la Biología (modelos de redes neuronales), la economía (modelos de mercado), la sociología (modelos de dinámica de opinión) y la ciencia de materiales (transiciones estructurales). Ha servido de base para establecer la teoría de sistemas complejos, donde las interacciones locales pueden llevar a un comportamiento global emergente. Esto es relevante en muchos contextos físicos y no físicos. Finalmente ha impulsado la educación y pedagogía, ya que el modelo de Ising se utiliza ampliamente como herramienta educativa en cursos de física estadística y materia condensada debido a su simplicidad y poder explicativo. Facilita la introducción de conceptos fundamentales como el ferromagnetismo, los puntos críticos y la termodinámica de sistemas de muchas partículas.

El modelo de Ising ha sido esencial para el avance de la Física teórica y experimental, proporcionando una comprensión profunda de las transiciones de fase y el comportamiento crítico en sistemas de muchas partículas.

Sopa de letras: MODELANDO LAS TRANSICIONES DE FASE

Soluciones: LICUEFACCIÓN HIDROTERMAL