Pensándolo bien...

Turing, en 1936, demostró que una función es computable si existe un algoritmo que pueda ejecutar la tarea de calcularla. De ello se infiere que, lo que denominamos proceso es todo aquello que puede definir una máquina de Turing. Al reverso, función computable es aquella para la que hay una máquina de Turing que puede calcularla. Se acepta la tesis de Iglesia-Turing de que un algoritmo está en correspondencia con lo que un modelo computacional puede hacer.

Iglesia y Turing demostraron, poco después de que Gödel evidenciara que las Matemáticas incompletas, que algunos problemas en matemáticas eran indecidibles. Se entiende por tal que no hay ningún algoritmo, por sofisticado que sea, que puede certificarnos una respuesta afirmativa o negativa. Ciertamente fue un golpe bajo para Hilbert, firme defensor de que las matemáticas ofrecían respuestas ordenadas e idealizadas. Claro que la propuesta de Turing, lejos de ser una piedra en el camino, resultó ser el motor que impulsó el desarrollo de la moderna computación. La máquina de Turing universal, capaz de simular cualquier otra máquina de Turing en cualquier entrada concebible. Von Newman ideó una arquitectura informática, que lleva su nombre, materializando el concepto universal de máquina de Turing y dio origen al ordenador convencional que conocemos.

Las máquinas de Turing son modelos matemáticos de computación que fueron propuestos por el matemático británico Alan Turing. Son fundamentales en la teoría de la computación y en la ciencia de la computación teórica, ya que formalizan el concepto de algoritmo y son capaces de simular cualquier cálculo que una computadora digital moderna pueda realizar.

Consiste en: 1) una cinta infinita, que es una secuencia de casillas que pueden contener un símbolo de un alfabeto finito. La cinta es infinita en ambas direcciones y se considera como el medio de almacenamiento de la máquina; 2) un cabezal de lectura/escritura, que puede leer y escribir símbolos en la cinta y puede moverse a la izquierda o a la derecha, una casilla cada vez; 3) Un conjunto finito de estados en los que puede encontrarse en un momento dado. Uno de estos estados es el estado inicial y hay uno o más estados finales; 4) Una tabla de transición, que define las reglas para la operación de la máquina. Para cada combinación de símbolo leído y estado actual, la tabla especifica: a) el símbolo que se escribirá en la cinta; b) la dirección en la que se moverá el cabezal (a izquierda o a derecha) y c) el nuevo estado de la máquina.

El funcionamiento básico de una máquina de Turing es simple:

1. La máquina comienza en el estado inicial y el cabezal de lectura/escritura está en la posición inicial en la cinta.

2. Lee el símbolo en la posición actual de la cinta.

3. De acuerdo con la tabla de transición, la máquina escribe un nuevo símbolo en la cinta, cambia su estado y mueve el cabezal a la izquierda o a la derecha.

4. Este proceso se repite hasta que la máquina llega a un estado final o entra en un ciclo infinito.

Con un ejemplo visualizamos mejor lo relatado. Imaginemos una máquina de Turing que tiene el alfabeto {0, 1} y la tarea que realiza consiste en cambiar todos los ceros a unos en una secuencia infinita de ceros y unos.

- Los estados son: {q0, q1}, donde q0 es el estado inicial y q1 es el estado final.

- La tabla de transición, consiste en:

  - (q0, 0) -> (1, D, q0) : Si el estado es q0 y el símbolo es 0, escribe 1, mueve el cabezal a la derecha y permanece en el estado q0.

  - (q0, 1) -> (1, D, q0) : Si el estado es q0 y el símbolo es 1, mueve el cabezal a la derecha y permanece en el estado q0.

  - (q0, ␣) -> (␣, D, q1) : Si el estado es q0 y el símbolo es un espacio en blanco, permanece en el espacio en blanco, mueve el cabezal a la derecha y cambia al estado q1.

Esta máquina continuará moviéndose a la derecha, cambiando todos los 0s a 1s, y eventualmente se detendrá cuando encuentre un espacio en blanco.

Las máquinas de Turing, aunque son modelos abstractos, han influido profundamente en el desarrollo de la teoría de la computación y en la comprensión de los límites de lo que las máquinas pueden calcular.

Una alternativa es la denominada máquina de Turing probabilística, que es una extensión del modelo clásico de la máquina de Turing que incorpora la probabilidad en su operación. Este tipo de máquina de Turing se emplea para modelar algoritmos probabilísticos y estudiar problemas de complejidad en la teoría de la computación.

Las características de una Máquina de Turing Probabilística vienen dadas por:

1. Cinta infinita: Igual que en una máquina de Turing clásica, la máquina tiene una cinta infinita dividida en casillas que pueden contener un símbolo de un alfabeto finito.
2. Cabezal de lectura/escritura: Puede leer y escribir símbolos en la cinta y moverse a la izquierda o a la derecha una casilla cada vez.
3. Conjunto finito de estados: La máquina tiene un conjunto de estados, incluyendo un estado inicial y uno o más estados de aceptación.
4. Tabla de transición probabilística: La diferencia clave con la máquina de Turing clásica es que, en lugar de tener una única acción definida para cada par de estado y símbolo, la máquina de Turing probabilística tiene una distribución de probabilidad sobre las posibles acciones.

Establezcamos, como ejemplo, una tabla de transición probabilística, que incluye para cada par (q, σ) no especifica una única acción, sino un conjunto de posibles acciones con sus respectivas probabilidades. Por ejemplo:

• Para el par (q₀, 0),
  • Con probabilidad 0.7, la máquina escribe '1', se mueve a la derecha y cambia al estado q₁​.
  • Con probabilidad 0.3, la máquina escribe '0', se mueve a la izquierda y permanece en el estado q₀​.

Funcionamiento de la Máquina de Turing Probabilística

1. La máquina comienza en el estado inicial con el cabezal de lectura/escritura en la posición inicial de la cinta.
2. Lee el símbolo en la posición actual de la cinta.
3. Usa la tabla de transición probabilística para determinar la siguiente acción basada en una distribución de probabilidad.
4. Escribe un nuevo símbolo en la cinta, mueve el cabezal y cambia el estado según la acción seleccionada.
5. Repite los pasos 2 – 4, hasta que alcanza un estado de aceptación o entra en un ciclo infinito.

Con un ejemplo de máquina de Turing probabilística visualizamos lo relatado. Consideremos una máquina de Turing probabilística simple que decide si una cadena binaria contiene más ceros que unos con una probabilidad de error aceptable.

• Estados: {q0,q1,q2}, donde q0​ es el estado inicial y q2​ es el estado de aceptación o final.
• Tabla de Transición:
  •  (q0​,0) → {(0.7,1,D,q0​),(0.3,1,I,q1​)}
  •  (q0​,1) → {(0.5,0,D,q0​),(0.5,1,D,q1​)}
  •  (q1​,0) → {(1.0,0,I,q2​)}
  • (q1,1) → {(1.0,1,I,q2)}

Las máquinas de Turing probabilísticas son importantes porque permiten el estudio de algoritmos que tienen elementos de aleatoriedad y proporcionan un marco para analizar problemas que pueden ser resueltos más eficientemente con algoritmos probabilísticos. Son una herramienta clave en el campo de la complejidad computacional, especialmente en la clase de complejidad BPP (Bounded-error Probabilistic Polynomial time), que incluye problemas que pueden ser resueltos por máquinas de Turing probabilísticas en tiempo polinómico con una probabilidad de error acotada.

Tanto las máquinas de Turing, como la inteligencia artificial (IA) están estrechamente relacionadas en la teoría de la computación y el desarrollo de algoritmos. Las máquinas de Turing proporcionan un modelo formal para entender lo que es computable, mientras que la IA utiliza estos principios para crear sistemas que pueden realizar tareas que requieren inteligencia humana.

La relación entre máquinas de Turing y la IA se evidencia contemplando los siguientes aspectos: a) Las máquinas de Turing son consideradas como el modelo de computación universal más básico. Cualquier algoritmo que puede ser implementado en un ordenador, puede ser simulado por una máquina de Turing. Esto incluye los algoritmos utilizados en IA, lo que implica que cualquier tarea que puede ser realizada por un programa de IA puede ser descrita formalmente en términos de una máquina de Turing; b) Muchos algoritmos de IA, especialmente en aprendizaje automático, pueden ser representados como procesos que una máquina de Turing podría ejecutar. Por ejemplo, los algoritmos de optimización y búsqueda utilizados en las redes neuronales y aprendizaje profundo son computables y, por tanto, pueden se pueden implementar en una máquina de Turing; c) La teoría de la computabilidad, que se basa en las máquinas de Turing, proporciona una base teórica para entender los límites de lo que puede ser calculado o aprendido por una máquina. Esto es crucial en IA para saber qué problemas son solucionables y cuáles no lo son, así como para entender la complejidad de los problemas.

En el contexto de la IA, se han desarrollado variaciones del modelo clásico de la máquina de Turing para abordar mejor las características de los sistemas inteligentes, como son las máquinas de Turing no deterministas que pueden hacer múltiples transiciones para una sola entrada, representando diferentes posibles caminos de ejecución. Esto es relevante en IA para la búsqueda de soluciones en problemas donde es necesaria la exploración de múltiples caminos. Además, como se mencionó anteriormente, las máquinas probabilísticas utilizan transiciones probabilísticas, lo que es útil para modelar algoritmos de IA que incluyen elementos de aleatoriedad, como algunos métodos de aprendizaje automático y algoritmos de optimización estocástica. Los modelos avanzados de IA a menudo requieren almacenar y recuperar grandes cantidades de datos. Las máquinas de Turing con memoria adicional o acceso a bases de datos externas pueden modelar esto, representando algoritmos que dependen del almacenamiento de datos históricos para el aprendizaje y la toma de decisiones.

Aunque en la práctica no se implementan algoritmos de IA directamente en máquinas de Turing, el concepto teórico de que cualquier algoritmo de IA puede ser simulado por una máquina de Turing proporciona una base sólida para el desarrollo de estos algoritmos. Ejemplos que evidencian la relación los encontramos en las redes neuronales, fundamentales en el aprendizaje profundo, que pueden ser vistas como un conjunto de funciones computables que una máquina de Turing puede simular. La retro-propagación y otros algoritmos de entrenamiento son computables y, por ende, formalmente describibles mediante una máquina de Turing. Por otro lado, los algoritmos genéticos, que se basan en la selección, mutación y recombinación para encontrar soluciones óptimas, pueden ser implementados por una máquina de Turing que simula estos procesos evolutivos. Y también, los sistemas expertos, que utilizan reglas y lógica para tomar decisiones, son esencialmente programas de computación que una máquina de Turing puede ejecutar, aplicando reglas y deducciones para llegar a conclusiones.

Con los avances en IA y el desarrollo de nuevos modelos computacionales, como los ordenadores cuánticos, la relación entre las máquinas de Turing y la IA, sigue siendo un área activa de investigación. Los ordenadores cuánticos, por ejemplo, amplían los límites de la computabilidad de maneras que aún están siendo exploradas teóricamente en relación con las máquinas de Turing. Las máquinas de Turing proporcionan la base teórica para la computación y los algoritmos de IA, mientras que la IA aplica estos principios para desarrollar sistemas que pueden realizar tareas complejas y simular la inteligencia humana.

La intersección entre las máquinas de Turing y la Química es un campo fascinante que abarca tanto la teoría de la computación como las aplicaciones prácticas en la Química. Esta relación se puede explorar desde varios ángulos, incluyendo la computación química, las simulaciones moleculares y el diseño de sistemas de computación basados en reacciones químicas.

Las máquinas de Turing proporcionan una base teórica para los algoritmos utilizados en la simulación de sistemas moleculares. Estos algoritmos son esenciales en la Química computacional para predecir propiedades y comportamientos de moléculas y materiales. Los métodos de simulación, como la dinámica molecular y los cálculos de estructura electrónica, se basan en algoritmos que pueden ser formalizados mediante una máquina de Turing.

Las reacciones químicas pueden ser modeladas computacionalmente utilizando algoritmos que siguen las reglas de una máquina de Turing. Esto incluye la simulación de mecanismos de reacción, la predicción de productos de reacción y la optimización de rutas sintéticas.

Un campo emergente es el de la computación química, donde se utilizan reacciones químicas para realizar operaciones de computación. Este enfoque está inspirado en la teoría de la computación de Turing y busca implementar procesos computacionales a través de reacciones químicas.

En teoría, es posible diseñar un sistema químico que funcione como una máquina de Turing. Esto implica usar moléculas y reacciones químicas para representar los estados, símbolos y transiciones de la máquina de Turing. Por ejemplo, diferentes concentraciones de reactivos y productos pueden representar diferentes estados y símbolos.

La lógica química utiliza reacciones químicas para implementar puertas lógicas y circuitos, que son los bloques fundamentales de los sistemas de computación. Las puertas lógicas químicas pueden realizar operaciones como AND, OR y NOT utilizando concentraciones de especies químicas para representar los valores de entrada y salida.

Imagen creada con ayuda de Chat GPT con DALL-E

Hay variadas aplicaciones prácticas, que evidencian el interés del tema. La química computacional, basada en algoritmos que pueden ser simulados por máquinas de Turing, es crucial en el diseño de medicamentos. Los algoritmos de modelado molecular y simulación ayudan a predecir cómo interactuarán las moléculas con los objetivos biológicos, acelerando el proceso de descubrimiento de fármacos. Los materiales que responden a estímulos externos, como cambios en la temperatura, pH o luz, pueden ser diseñados utilizando simulaciones computacionales. Estos materiales inteligentes tienen aplicaciones en medicina, electrónica y energía. Los sintetizadores automáticos de productos químicos, que utilizan algoritmos para planificar y ejecutar la síntesis de compuestos, se basan en principios computacionales que pueden ser formalizados mediante máquinas de Turing. Estos sistemas pueden automatizar la producción de una amplia variedad de productos químicos.

Construir una máquina de Turing, por ejemplo, para sintetizar agua, implica diseñar un modelo computacional que simule el proceso de combinar hidrógeno y oxígeno para formar agua. Aunque en la práctica no se utilizan máquinas de Turing para realizar síntesis química directamente, podemos utilizar el concepto teórico para describir los pasos y las transiciones necesarias para esta reacción química.

La reacción química básica para sintetizar agua es: 2H₂+O₂→2H₂O. Los componentes de la máquina de Turing son:

1. Cinta: La cinta de la máquina de Turing representará las moléculas de hidrógeno (H_2​) y oxígeno (O₂​) y el agua (H₂O).
2. Símbolos: Los símbolos en la cinta pueden ser H, O, y A (representando H₂ O₂ y H₂​O).
3. Estados: La máquina tendrá varios estados para controlar el proceso de síntesis.
   • q0​: Estado inicial.
   • q1​: Estado de búsqueda de hidrógeno.
   • q2​: Estado de búsqueda de oxígeno.
   • q3​: Estado de síntesis.
   • q_f​: Estado final (aceptación).
4. Transiciones: Las reglas de transición definirán cómo se mueve el cabezal de lectura/escritura y cómo se transforman los símbolos en la cinta.

Diseñamos una tabla de transición simplificada:

1. Comenzamos en el estado inicial q0​.
2. Buscamos una molécula de hidrógeno en el estado q1​.
3. Cambiamos al estado q2​ cuando encontramos un hidrógeno.
4. Buscamos una molécula de oxígeno en el estado q2​.
5. Cambiamos al estado q3​ cuando encontramos un oxígeno.
6. Realizamos la síntesis en el estado q3​, reemplazando los símbolos H y O por A (agua).
7. Volvemos al estado inicial q0​ y repetimos el proceso.
8. Terminamos en el estado q_f ​ cuando se sintetiza el agua suficiente.

Que puede verse así:

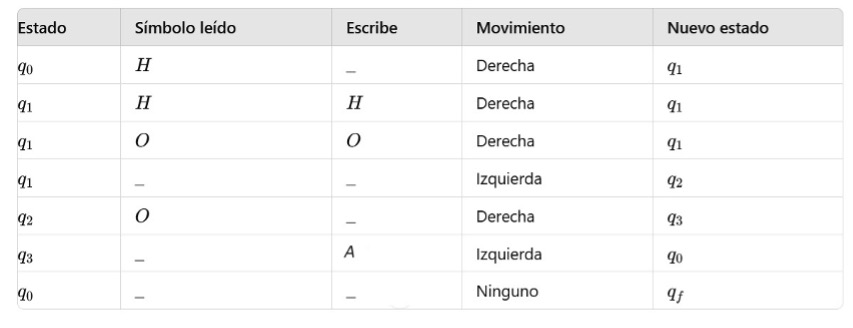
Descripción del Proceso

1. Inicio: La máquina comienza en el estado q0​ y busca un H en la cinta.
2. Búsqueda de Hidrógeno: en el estado q1​, la máquina busca un símbolo H. Cuando lo encuentra, lo marca y se mueve al estado q2​.
3. Búsqueda de Oxígeno: en el estado q2​, la máquina busca un símbolo O. Cuando lo encuentra, lo marca y se mueve al estado q3​.
4. Síntesis de Agua: en el estado q3​, la máquina escribe A en la posición actual, indicando que se ha formado una molécula de agua.
5. Reinicio: La máquina vuelve al estado q0​ para repetir el proceso o al estado final q_f​, si se ha completado la tarea.

Esta máquina de Turing es una simplificación extrema y no captura la complejidad de las reacciones químicas reales, incluyendo las condiciones necesarias de temperatura, presión, catalizadores, etc. para que el proceso tenga lugar, así como los detalles moleculares específicos. Sin embargo, proporciona una visión teórica de cómo un proceso químico se puede representar en un modelo computacional formal. Este modelo teórico es útil en la intersección de la computación y la Química, proporcionando una base para la creación de algoritmos y sistemas que simulan y optimizan procesos químicos en la investigación y la industria.

La investigación continua en este ámbito e incluye el desarrollo de nuevos modelos y algoritmos para mejorar la eficiencia y precisión de las simulaciones químicas. Igualmente se exploran nuevas formas de computación basadas en principios químicos, con el objetivo de crear sistemas de computación más rápidos y eficientes que los actuales.

Sopa de letras: MÁQUINAS QUÍMICAS DE TURING

Soluciones: LA ERA DE LOS DATOS MULTIMODALES