Pensándolo bien...
No es nada nuevo que la IA ha irrumpido en todas las esferas de actividad humana. No es nada nuevo, por cuanto reconocer su importancia desde los premios Nobel, indica que ya han realizado un recorrido determinante. Eso exige tiempo y reposo para que su aportación sea reconocida como de importancia suficiente para la Humanidad.
En Física, el Premio Nobel es para John J. Hopfield y Geoffrey E. Hinton, a los que se reconoce, textualmente "por los descubrimientos e invenciones fundamentales que permiten el aprendizaje automático con redes neuronales artificiales". Tanto Hopfield como Hinton han sido reconocidos por su labor desde 1980, centrada en el desarrollo de redes neuronales artificiales. Se reconoce que sus trabajos establecieron las bases para que en 2010 se diera nacimiento a la revolución del aprendizaje automático, rama de la Inteligencia Artificial que ha disparado su evolución y utilidad.
Hay que remontarse al modelo de Ising, que es un concepto clave en la física estadística, propuesto por el físico alemán Ernst Ising en 1925, basado en una idea desarrollada inicialmente por su asesor Wilhelm Lenz. El modelo de Ising fue propuesto originalmente para estudiar el magnetismo en materiales, pero con el tiempo ha encontrado aplicaciones en muchas otras áreas, desde física hasta biología y computación. Fue recompensado en 1968 con el Nobel de Química.
Lo hemos tratado repetidas veces en esta sección, intentando escudriñar en las interioridades de las redes neuronales. Resumimos sus elementos clave, que permitirán entender las aportaciones que ahora se reconocen con el Nobel. El modelo de Ising describe un sistema de espines que, como es conocido, pueden tener dos estados posibles: "arriba" (+1) o "abajo" (-1). Los espines están dispuestos en una “rejilla” o matriz (regularmente en 1D, 2D o 3D) y cada espín interactúa solo con sus espines vecinos más cercanos. La energía del sistema se determina en función de cómo se alinean los espines entre sí, lo que refleja su tendencia a alinearse en la misma dirección o en direcciones opuestas.
La física del sistema se enmarca en que los espines representan los momentos magnéticos de partículas atómicas en una red, que pueden orientarse en dos direcciones. El sistema tiende a minimizar su energía total y la energía de interacción entre dos espines vecinos depende de si están alineados en la misma dirección o en direcciones opuestas. A bajas temperaturas, los espines tienden a alinearse, lo que corresponde al estado ferromagnético (ordenado). A altas temperaturas, los espines se orientan aleatoriamente, lo que corresponde al estado paramagnético (desordenado).
El Hamiltoniano del modelo de Ising viene dado por
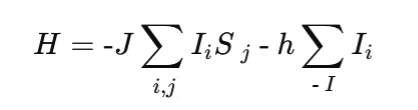
- Ii representa el estado del espín en la posición i (que puede ser +1 o -1).
- J es un parámetro que representa la fuerza de interacción entre espines vecinos. Si J >0, los espines tienden a alinearse, lo que describe un sistema ferromagnético.
- i, j, denota que la suma se realiza sobre espines vecinos.
- h es un campo externo que puede influir en la alineación de los espines.
- El primer término describe la interacción entre los espines vecinos, y el segundo término describe la influencia de un campo magnético externo.
El modelo de Ising es famoso porque exhibe las transiciones de fase. En el caso más simple, cuando no hay campo externo (h=0), se observa una transición entre un estado ferromagnético ordenado (a bajas temperaturas) y un estado paramagnético desordenado (a altas temperaturas). En el caso 2D, esta transición ocurre a una temperatura crítica específica.
Aunque el modelo de Ising fue diseñado para estudiar el magnetismo, ha demostrado ser extremadamente versátil y ha encontrado aplicaciones en muchas otras disciplinas, como en Biología y Genética en las que se ha utilizado para describir la interacción de genes y el comportamiento de proteínas en redes biológicas, donde los individuos (análogos a espines) pueden estar en un estado "arriba" o "abajo" en función de la influencia de sus vecinos. En Neurociencia, el modelo de Ising ha sido aplicado a la construcción de redes neuronales para modelar cómo las neuronas pueden interactuar de manera cooperativa o competitiva. Específicamente, en redes como la de Hopfield, que mencionamos antes, se utiliza una variante del modelo de Ising para describir el almacenamiento de patrones en la memoria asociativa. En economía y sociología, el modelo de Ising también se ha utilizado para aplicarlo a modelos sociales y económicos, como el colectivo en sistemas donde los individuos tienden a seguir la opinión de sus vecinos, lo que da lugar a la propagación de creencias, modas, o tendencias de mercado. En problemas de optimización el modelo de Ising es útil en resolución los ciertos problemas, como el de satisfacción booleana, donde se busca encontrar configuraciones que minimicen una función de energía. Esto ha encontrado aplicaciones en inteligencia artificial y computación. En teoría de redes, el modelo de Ising se ha utilizado para estudiar la dinámica de redes complejas, como las interacciones en redes sociales o de comunicación, donde los "nodos" del sistema (personas o servidores) pueden influirse mutuamente de manera similar a los espines.
El modelo de Ising también sirvió de base para desarrollar modelos más complejos, como el Modelo de Potts, que generaliza el modelo de Ising permitiendo que cada espín tome más de dos valores posibles y es relevante en áreas donde existen múltiples estados o fases posibles.
Ha sido decisivo en el desarrollo de teorías de la física moderna, como la teoría de transiciones de fase y fenómenos críticos en física estadística. El análisis matemático de este modelo ha permitido obtener una comprensión más profunda de cómo ocurren las transiciones de fase en muchos sistemas físicos y cómo las fluctuaciones juegan un papel importante en estos procesos. el interés es de tal talla que en realidad es una herramienta clave para modelar y entender la interacción entre elementos en muchos tipos de sistemas complejos, desde la física de materiales hasta la biología, la sociología y la inteligencia artificial, que ahora alcanza el estatus que otorga el Nobel.
En la expresión del hamiltoniano del modelo de Ising, el sumatorio indica la suma de todas las interacciones posibles, que en términos de espín serán concordancias o discordancias, lo que genera un valor numérico que, en el caso de concordar todos, será un numero positivo grande y en el caso de que sean discordantes obtendremos un número negativo grande. El signo menos indica que tratamos las concordancias como decrementos de la energía de interacción y las discordancias como incrementos de la misma. Si la energía de interacción es elevada, debido a que los espines son discrepantes, los campos magnéticos generados por los átomos individuales concordantes quedan anulados y no exhiben comportamiento magnético, Pero cuando la interacción es baja, debido a que hay muchos espines concordantes, el efecto acumulativo de los campos magnéticos individuales sumados (espines alineados predominantemente) la materia exhibirá un comportamiento magnético, el ferromagnetismo.
Lo importante del modelo de Ising es que asume el tratamiento cuántico que describe cómo un metal se convierte en un imán. Lo sorprendente, que destacamos especialmente, es cómo el modelo de Ising que conduce al modelo neurológico de Hopfield. Aparentemente no hay ninguna relación, pero sirvió de inspiración del modelo de redes neuronales de Hopfield. Es éste un modelo clásico en el que Hopfield reinterpreta el modelo de interacción de espines atómicos en un metal, como un entorno de interacciones, ahora comunicativas, entre las neuronas. El resultado fue una red neuronal que obedecía a reglas simples y que razonablemente describía una información almacenada y aprendida que permitía recordarla y recuperarla. Las islas de espines correlacionadas se convertían en configuraciones que representaban a la memoria.
El hecho seminal es que se sabe que las neuronas se comunican a través de disparos en los que se liberan neurotransmisores en las uniones, sinapsis, que conectan a aquéllas. Hopfield simplificó esta transmisión suponiendo que entre las neuronas hay una “fuerza” que representa la interacción entre ellas, que es el factor J del Hamiltoniano de Ising. Los matices son de interés, porque en el modelo de Ising, los espines solo interaccionan con sus vecinos inmediatos, pero en nuestro cerebro las neuronas están conectadas con otras innumerables neuronas. La clave, pues es el concepto de disparo de la neurona en el modelo de Hopfield y el espín del modelo de Ising. Si la neurona se encuentra en un estado “arriba”, se asume que ha disparado una señal electroquímica, y si esta hacia “abajo, entonces no ha disparado todavía.
Hopfield propuso una ecuación de estado (un hamiltoniano) similar al de Ising que incluía a todas las neuronas conectadas. La matemática implicada es la misma en ambos modelos. Dos neuronas que disparan o no disparan al unísono, incrementan su conexión. Si las neuronas actúan de manera opuesta reducen el estado de conexión. Lo denotaríamos así
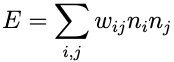donde apreciamos que hemos reemplazado la variable de espín Si por la variable neurona, ni . No se incluyen efectos externos (en segundo término del hamiltoniano de Ising) y en lugar de un único término de interacción, J, que describe la relación entre cada par, ahora se considera un término para cada valor, wi j,, que expresa la potencial interacción entre dos cualesquiera neuronas del cerebro y no solo las inmediatas próximas. Este peso, wi j, indica la intensidad con la que una neurona se conecta con otra. El modelo de Hopfield se centra en determinar estos pesos. El patrón de las fuerzas de conexión lo establece el conjunto de estados distintos.
En un primer estadio, estas redes se diseñaron en la forma supervisada, consistente en que en la determinación de los pesos, se actuaba vigilando que la respuesta fuera la esperada, entrenando las redes con datos conocidos. Ciertamente se manejaba una estructura capaz de aprender y recordar. Lo único limitante eran los datos con los que entrenar al sistema para buscar pesos significativos en el área en que se aplicaba. Surgieron las redes no supervisadas en las que el entrenamiento lo hacen ellas solas, para generar nuevos recuerdos. Tratar grandes cantidades de datos sin categorías previas preexistentes, implica que la red adquiere una “inteligencia” identificando clases en las que encajar los datos. La red de Hopfield es una traslación de conceptos de un campo a otro y muestra una conexión entre la física y la neurología. Las analogías entre campos del conocimiento son un arte. Nunca son completas las analogías. En este caso, tampoco, porque las neuronas están interconectadas de forma mucho más compleja que los átomos de un metal. Pero la analogía permitió que los neurólogos incorporaran la complejidad de los circuitos neuronales al modelo análogo y adecuarlo y mejorarlo. Un trabajo de premio Nobel, sin duda.
La característica clave de una red de Hopfield es su capacidad de almacenar múltiples patrones y luego recuperar el patrón correcto, incluso si se le proporciona una entrada imperfecta o ruidosa. Cuando se presenta un patrón incompleto o distorsionado, la red actualiza progresivamente el estado de sus neuronas, buscando una configuración que se asemeje al patrón almacenado más cercano. Este proceso es conocido como relajación hacia un estado de equilibrio, donde la red converge hacia el patrón que más se parece a la entrada inicial.
Esta estructura es especialmente útil en aplicaciones de memoria asociativa y ha sido la base para el desarrollo de otros modelos más complejos en inteligencia artificial y redes neuronales y han inspirado una amplia gama de aplicaciones en diversas áreas, tanto en inteligencia artificial como en otras disciplinas, como reconocimiento de patrones y corrección de errores, reconocimiento de voz reconocimiento de caracteres (OCR) o reconocimiento de imágenes.
La red de Hopfield se diseñó originalmente para funcionar como una memoria asociativa, en la que un patrón se asocia con otro, de manera que cuando se le presenta un estímulo parcial, la red es capaz de recordar y recuperar el patrón completo. Ejemplos el almacenamiento de información visual o auditiva en sistemas neuronales, donde un estímulo parcial (como una parte de una imagen o un sonido) desencadena el recuerdo de la totalidad o los modelos de memoria humana en neurociencia computacional, donde se simulan ciertos aspectos de cómo el cerebro humano asocia recuerdos y los recupera cuando se le da una pista incompleta.
Otro campo de aplicación es la corrección de errores en telecomunicaciones o corrección de errores de código en transmisión digital. Si un mensaje o conjunto de datos se transmite con ruido, la red de Hopfield puede ayudar a recuperar los datos correctos usando su capacidad para encontrar el patrón almacenado más cercano. Es una herramienta valiosa para la optimización de problemas NP-completos como el problema del viajante, para encontrar rutas de viaje óptimas o casi óptimas o los problemas de satisfactibilidad booleana, en los que se busca encontrar una configuración de variables que haga verdadera una fórmula lógica compleja. Su contribución ha sido decisiva en el procesamiento distribuido y memoria compartida y distribuida, donde la red emula cómo diferentes nodos de un sistema pueden acceder y modificar el mismo "almacenamiento" de patrones.
En neurociencia y psicología computacional, la red de Hopfield ha sido usada como modelo para entender cómo el cerebro humano podría funcionar en términos de recuperación de recuerdos. Sus mecanismos tienen paralelos con ciertos procesos cognitivos, como la simulación de memoria a largo plazo o la simulación de redes neuronales biológicas, en que se utiliza para modelar procesos como el sueño o la memoria en modelos de sistemas nerviosos, ya que estos también muestran tendencias hacia la estabilización de estados en el cerebro.
Las redes de Hopfield han servido como base para otros modelos más avanzados, como las Redes de Boltzmann y las Redes de Creencia Profunda (Deep Belief Networks), que tienen aplicaciones en aprendizaje profundo (deep learning). Estas redes se usan enreconocimiento de imágenes complejas, en tareas como la clasificación de imágenes o el reconocimiento facial y en optimización y generación de datos en tareas como el análisis de grandes conjuntos de datos o en aplicaciones creativas como la generación de texto o imágenes.
Las redes de Hopfield se han utilizado en sistemas de diagnóstico médico para identificar patrones asociados con enfermedades en señales médicas ruidosas o incompletas. Un ejemplo es la interpretación de electrocardiogramas, para detectar irregularidades o señales distorsionadas que podrían indicar condiciones cardíacas, análisis de imágenes médicas, como radiografías o escáneres, donde partes de la imagen pueden estar afectadas por ruido. La red de Hopfield ha inspirado una gran variedad de aplicaciones, tanto en el campo de la inteligencia artificial como en áreas prácticas que requieren sistemas de memoria y reconocimiento robustos.
Si Hopfield creó una memoria asociativa en 1982, con las funciones de almacenar y reconstruir imágenes y otros tipos de patrones en los datos, Hinton, por su parte, desarrolló un método que permite a una máquina encontrar propiedades en los datos, pero de forma autónoma y, contribuyendo a identificar elementos concretos en las imágenes. Podemos rec0onocer imágenes y asociarlas con las almacenadas en la memoria, procedentes de experiencias pasadas. Las neuronas, en número de 80.000 millones de neuronas que están conectadas entre sí nos proporcionan una capacidad cognitiva
No cabe duda de que las investigaciones de Hinton han aliviado el camino para que surjan sistemas de inteligencia artificial como el conocido ChatGPT. No cabe duda de que Hopfield y Hinton han aportado herramientas que facilitan a los humanos la toma de decisiones de forma más rápida y confiable a la hora de diagnosticar, incluidas las enfermedades.
Geoffrey Hinton es otro de los pioneros en el campo de la inteligencia artificial, ha hecho contribuciones fundamentales a las redes neuronales y, en particular, al desarrollo del aprendizaje profundo (deep learning). A lo largo de su carrera, Hinton ha sido una de las figuras más influyentes en la evolución de las redes neuronales artificiales y su resurgimiento en las últimas décadas.
Hinton fue uno de los primeros en popularizar el uso del algoritmo de retropropagación del error en redes neuronales profundas, una técnica clave para entrenar redes neuronales multicapa. Aunque el algoritmo de retropropagación fue introducido por otros investigadores, Hinton lo aplicó con éxito al entrenamiento de redes neuronales en 1986, junto con David Rumelhart y Ronald J. Williams. Este algoritmo permitió que las redes neuronales aprendieran de manera más efectiva ajustando los pesos de las conexiones neuronales a medida que se minimizan los errores en las predicciones de salida.
Retropropagación es el proceso mediante el cual el error se propaga hacia atrás desde las capas de salida hasta las capas anteriores de la red, permitiendo que los pesos de las conexiones neuronales se actualicen en función del gradiente descendente. Esto permite que las redes neuronales aprendan de manera supervisada y ajusten su comportamiento de manera más precisa a lo largo de muchas capas. En 2006, Hinton revolucionó el campo con la introducción de las Redes de Creencias Profundas (Deep Belief Networks, DBNs), un tipo de arquitectura que utiliza una combinación de máquinas de Boltzmann restringidas y aprendizaje no supervisado. Antes de este trabajo, las redes neuronales profundas eran difíciles de entrenar debido a problemas con el gradiente y la falta de poder computacional. Hinton demostró que se podía preentrenar las redes de forma no supervisada, capa por capa, utilizando una red de máquinas de Boltzman y luego afinar toda la red con retropropagación supervisada. Las máquinas de Boltzmann restringidas, son modelos generativos que pueden aprender representaciones internas de los datos. Hinton las usó como bloques constructivos para las redes de creencias profundas, lo que permitió a las redes neuronales profundas aprender características jerárquicas y representar información más abstracta y compleja. Las Redes de Creencias Profundas, introdujeron el concepto de preentrenamiento no supervisado seguido de ajuste fino supervisado, lo que permitió un entrenamiento más eficiente de redes profundas. Esto resultó en mejoras importantes en tareas como la clasificación de imágenes y el reconocimiento de patrones. Aunque las redes neuronales convolucionales fueron originalmente propuestas por Yann LeCun en la década de 1990, Hinton jugó un papel crucial en el resurgimiento del aprendizaje profundo y el reconocimiento de imágenes a través de redes profundas. En 2012, el equipo de Hinton, incluido Alex Krizhevsky y Ilya Sutskever, desarrolló AlexNet, una CNN profunda que ganó la competición de clasificación de imágenes ImageNet con un rendimiento notable, superando por un amplio margen todos los enfoques tradicionales de la época. El éxito de AlexNet marcó un hito en el campo del aprendizaje profundo y demostró el poder de las redes neuronales profundas entrenadas con grandes cantidades de datos y con hardware especializado (como GPUs). Este avance fue clave para el renacimiento de las redes neuronales y su aplicación a gran escala en tareas de visión por ordenador, reconocimiento de voz, procesamiento del lenguaje natural, entre otras.
Imagen creada con ayuda de ChatGPT con DALL-E
Hinton también ha sido fundamental en el campo del procesamiento del lenguaje natural (NLP) al ayudar a introducir la idea de vectores de palabras (word embeddings), donde las palabras son representadas como vectores en un espacio continuo de características. Esto ayudó a mejorar significativamente los modelos de NLP, permitiendo que las palabras que tienen significados similares tengan representaciones vectoriales similares. Aunque modelos como Word2Vec y GloVe fueron propuestos por otros investigadores, Hinton fue una influencia clave en la idea de representar características abstractas en espacios continuos, un concepto que también subyace en el funcionamiento de muchas redes neuronales profundas modernas.
Hinton introdujo una técnica llamada dropout, que es un método para prevenir el sobreajuste en redes neuronales profundas. El dropout funciona "apagando" aleatoriamente una fracción de las neuronas durante cada actualización del entrenamiento, lo que fuerza a la red a aprender representaciones más robustas y a no depender de conjuntos específicos de neuronas. Este enfoque ahora es ampliamente utilizado en el entrenamiento de redes neuronales profundas. El dropout ha demostrado ser una técnica extremadamente efectiva para mejorar el rendimiento de las redes profundas, especialmente cuando se entrenan con conjuntos de datos relativamente pequeños en comparación con la cantidad de parámetros de la red.
En 2017, Hinton propuso una arquitectura innovadora llamada Capsule Networks (Redes de Cápsulas), que busca mejorar las limitaciones de las redes neuronales convolucionales tradicionales (CNNs) en la detección de relaciones espaciales entre objetos y partes de objetos. Las redes de cápsulas intentan mantener la estructura espacial y las relaciones entre diferentes características en las imágenes, lo que podría hacerlas más robustas ante transformaciones como rotaciones o cambios de perspectiva. Aunque las Capsule Networks, aún no han alcanzado la misma popularidad que otras arquitecturas profundas, representan un área prometedora de investigación para mejorar el rendimiento en el reconocimiento de patrones visuales complejos.
Hinton también ha sido una figura clave en el desarrollo de técnicas como “distillation” y “knowledge transfer”, donde el conocimiento adquirido por un modelo grande y complejo se transfiere a un modelo más pequeño. Esto es útil para hacer que los modelos sean más eficientes y aplicables en dispositivos con recursos limitados, como los teléfonos móviles.
Geoffrey Hinton no solo ha realizado contribuciones teóricas importantes, sino que ha tenido un papel central en el renacimiento y expansión del aprendizaje profundo y ha ayudado a que la inteligencia artificial moderna sea una tecnología viable y exitosa en la práctica. Sus trabajos influyeron en el desarrollo de asistentes virtuales, como Siri o Alexa, en sistemas de visión por ordenador usados en reconocimiento facial, clasificación de imágenes y conducción autónoma, en sistemas de recomendación, como los usados por empresas como Netflix y Amazon. Hinton ha sido un defensor y promotor clave de las redes neuronales profundas, un campo que a mediados del siglo XX estaba en gran parte desacreditado, pero que gracias a sus contribuciones se convirtió en el núcleo de la IA moderna.
No está exento de reflexiones humanas profundas sobre las consecuencias potenciales de la IA admitió que también se abren puertas a situaciones peligrosas y riesgosas. Hinton, en 2023 renunció a su puesto como asesor de Google y alertó los riesgos del desbocado desarrollo de la IA. Su principal argumento es "No tenemos experiencia sobre lo que es tener cosas más inteligentes que nosotros", como ha declarado a los informadores que han conectado con él, tras la concesión del Nobel. “la amenaza de que estas cosas se salgan de control". Hinton pronostica que "Mi suposición es que, dentro de cinco o 20 años, habrá una probabilidad del 50% de que tengamos que afrontar el problema de que la inteligencia artificial intente tomar el control de nuestras vidas", dijo.
El contexto de la renuncia de Hinton se configura como que había trabajado en Google durante aproximadamente una década, ayudando a la empresa a impulsar sus capacidades en inteligencia artificial. Sin embargo, en mayo de 2023, anunció su renuncia y comenzó a hablar abiertamente sobre sus preocupaciones en torno al desarrollo desmedido de la IA. En sus declaraciones, Hinton expresó su temor de que los avances recientes en IA, especialmente en modelos como GPT-4 y otros sistemas de IA generativa, podrían tener efectos profundamente negativos si no se gestionan adecuadamente. Las razones de la advertencia de Hinton se centran en que el rápido progreso en la IA podría llevar a la creación de sistemas que no solo superen las capacidades humanas en varias áreas, sino que también escapen al control humano. Según él, la velocidad con la que la IA está evolucionando podría generar una serie de problemas impredecibles, desde el desplazamiento masivo de empleos hasta amenazas más amplias para la estabilidad social. Hinton también expresó preocupación sobre el desarrollo de una posible Inteligencia Artificial General (AGI), es decir, sistemas de IA que no solo son expertos en tareas específicas, sino que pueden aprender y adaptarse de manera similar a los humanos. Según Hinton, si las IA alcanzan un nivel de inteligencia comparable o superior al de los humanos, podría ser extremadamente difícil controlar sus acciones y objetivos. Otro de los puntos destacados por Hinton es que las IA avanzadas, como los modelos de lenguaje natural, podrían ser utilizadas para crear y difundir desinformación a gran escala. Los modelos de IA generativa, como los que desarrollan texto, imágenes y videos sintéticos, ya están en uso para crear contenidos que podrían engañar a la opinión pública, desde noticias falsas hasta campañas de manipulación. Hinton también señaló que la competencia global en el desarrollo de IA está impulsando a las empresas y países a avanzar a un ritmo acelerado, sin suficiente consideración por las implicaciones éticas. Esto puede generar una "carrera armamentista de IA", en la que los desarrolladores priorizan el progreso tecnológico sobre las consideraciones de seguridad, lo que podría llevar a consecuencias graves si no se aplican regulaciones adecuadas. Hinton advirtió que los avances en IA podrían reemplazar a muchos trabajos en diversas industrias, desde el transporte hasta el sector de servicios, lo que podría desestabilizar economías y generar desigualdades sociales aún más profundas. Aunque el desarrollo de la IA tiene el potencial de crear nuevos trabajos, Hinton expresó su preocupación por el ritmo al que estos cambios están ocurriendo.
La renuncia de Hinton y sus declaraciones resonaron profundamente en la comunidad tecnológica y científica, ya que Hinton ha sido considerado uno de los "padres del aprendizaje profundo" y su legado está vinculado a muchos de los avances que hoy son el núcleo de las aplicaciones modernas de IA. Google, en respuesta a las declaraciones de Hinton, reafirmó su compromiso con el desarrollo responsable de la IA y destacó los esfuerzos que la compañía ha hecho para garantizar la seguridad y la ética en el desarrollo de tecnologías de IA. Otros expertos en IA han coincidido con las preocupaciones de Hinton, alertando que las regulaciones y las consideraciones éticas no han avanzado al mismo ritmo que la tecnología, lo que deja un vacío en términos de control y seguridad.
En varias entrevistas, Hinton expresó que se siente algo culpable por haber contribuido al desarrollo de tecnologías que podrían convertirse en una amenaza para la humanidad. Él mismo comparó su situación con la de Robert Oppenheimer, uno de los creadores de la bomba atómica, en el sentido de que contribuyó a una innovación científica sin prever completamente sus implicaciones destructivas. En suma, en 2023, Geoffrey Hinton dejó Google y advirtió sobre los riesgos inherentes al desarrollo desmedido de la inteligencia artificial, destacando los peligros de la creación de sistemas que podrían escapar al control humano, la propagación de desinformación, el impacto en el empleo y la competencia internacional desregulada en IA.
Todo un recital de cómo la modernidad ha impactado en el Nobel de una forma rotunda en todas las esferas de actividad humana. La Ciencia inicia una etapa nueva en la que se espera una especial sensibilidad y capacidad de adaptación de todas las disciplinas que deberán ordenar apropiadamente los avances propuestos y las restricciones éticas que garanticen que no solo es desarrollo, sino progreso, lo que se propicia.
Sola de letras: LA IA EN LOS NOBEL (Y II)
Soluciones: LA IA EN LOS NOBEL, I